Principle of explosion
The principle of explosion, (Latin: ex falso quodlibet or ex contradictione sequitur quodlibet, "from a contradiction, anything follows") or the principle of Pseudo-Scotus, is the law of classical logic and intuitionistic and similar systems of logic, according to which any statement can be proven from a contradiction.[1] That is, once a contradiction has been asserted, any proposition (or its negation) can be inferred from it. In symbolic terms, the principle of explosion can be expressed in the following way (where "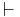 " symbolizes the relation of logical consequence):
" symbolizes the relation of logical consequence):
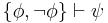
- or
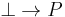 .
.
This can be read as, "If one claims something is both true (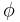 ) and not true (
) and not true (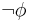 ), one can logically derive any conclusion (
), one can logically derive any conclusion ( )."
)."
Contents |
Arguments for explosion
An informal statement of the argument for explosion is this: Consider two inconsistent statements, “All lemons are yellow” and "All lemons are not yellow", and suppose for the sake of argument that both are true. We can then prove anything, for instance that Santa Claus exists: Since the statement that "All lemons are yellow and all lemons are not yellow" is true, we can infer that all lemons are yellow. And from this we can infer that the statement “Either all lemons are yellow or Santa Claus exists” is true (one or the other has to be true for this statement to be true, and we just showed that it is true that all lemons are yellow, so this expanded statement is true). And since either all lemons are yellow or Santa Claus exists, and since all lemons are not yellow, (this was our first premise), it must be true that Santa Claus exists.
In more formal terms, there are two basic kinds of argument for the principle of explosion, semantic and proof-theoretic.
The semantic argument
The first argument is semantic or model-theoretic in nature. A sentence  is a semantic consequence of a set of sentences
is a semantic consequence of a set of sentences 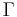 only if every model of
only if every model of 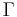 is a model of
is a model of  . But there is no model of the contradictory set
. But there is no model of the contradictory set 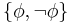 . A fortiori, there is no model of
. A fortiori, there is no model of 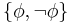 that is not a model of
that is not a model of  . Thus, vacuously, every model of
. Thus, vacuously, every model of 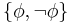 is a model of
is a model of  . Thus
. Thus  is a semantic consequence of
is a semantic consequence of 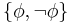 .
.
The proof-theoretic argument
The second type of argument is proof-theoretic in nature. Consider the following derivations:
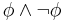
- assumption
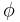
- from (1) by conjunction elimination
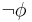
- from (1) by conjunction elimination
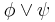
- from (2) by disjunction introduction
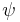
- from (3) and (4) by disjunctive syllogism
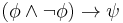
- from (5) by conditional proof (discharging assumption 1)
This is just the symbolic version of the informal argument given above, with  standing for "all lemons are yellow" and
standing for "all lemons are yellow" and  standing for "Santa Claus exists". From "all lemons are yellow and all lemons are not yellow" (1), we infer "all lemons are yellow" (2) and "all lemons are not yellow" (3); from "all lemons are yellow" (2), we infer "all lemons are yellow or Santa Claus exists" (4); and from "all lemons are not yellow" (3) and "all lemons are yellow or Santa Claus exists" (4), we infer "Santa Claus exists" (5). Hence, if all lemons are yellow and all lemons are not yellow, then Santa Claus exists.
standing for "Santa Claus exists". From "all lemons are yellow and all lemons are not yellow" (1), we infer "all lemons are yellow" (2) and "all lemons are not yellow" (3); from "all lemons are yellow" (2), we infer "all lemons are yellow or Santa Claus exists" (4); and from "all lemons are not yellow" (3) and "all lemons are yellow or Santa Claus exists" (4), we infer "Santa Claus exists" (5). Hence, if all lemons are yellow and all lemons are not yellow, then Santa Claus exists.
Or:
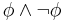
- hypothesis
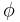
- from (1) by conjunction elimination
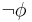
- from (1) by conjunction elimination
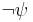
- hypothesis
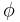
- reiteration of (2)
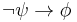
- from (4) to (5) by deduction theorem
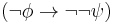
- from (6) by contraposition
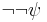
- from (3) and (7) by modus ponens
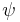
- from (8) by double negation elimination
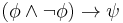
- from (1) to (9) by deduction theorem
Or:
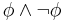
- assumption
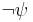
- assumption
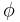
- from (1) by conjunction elimination
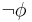
- from (1) by conjunction elimination
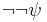
- from (3) and (4) by reductio ad absurdum (discharging assumption 2)
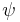
- from (5) by double negation elimination
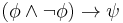
- from (6) by conditional proof (discharging assumption 1)
Addressing the principle
Paraconsistent logics have been developed that allow for sub-contrary forming operators. Model-theoretic paraconsistent logicians often deny the assumption that there can be no model of 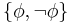 and devise semantical systems in which there are such models. Alternatively, they reject the idea that propositions can be classified as true or false. Proof-theoretic paraconsistent logics usually deny the validity of one of the steps necessary for deriving an explosion, typically including disjunctive syllogism, disjunction introduction, and reductio ad absurdum.
and devise semantical systems in which there are such models. Alternatively, they reject the idea that propositions can be classified as true or false. Proof-theoretic paraconsistent logics usually deny the validity of one of the steps necessary for deriving an explosion, typically including disjunctive syllogism, disjunction introduction, and reductio ad absurdum.
See also
- Dialetheism – belief in the existence of true contradictions
- Law of excluded middle – every proposition is either true or not true
- Law of noncontradiction – no proposition can be both true and not true
- Paraconsistent logic – a modal logic used to address contradictions
- Paradox of entailment – a seeming paradox derived from the principle of explosion
- Reductio ad absurdum – concluding that a proposition is false because it produces a contradiction
- Trivialism – the belief that all statements of the form "P and not-P" are true
References
- ^ Carnielli, W. and Marcos, J. (2001) "Ex contradictione non sequitur quodlibet" Proc. 2nd Conf. on Reasoning and Logic (Bucharest, July 2000)